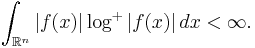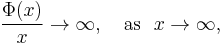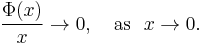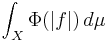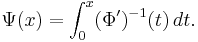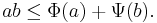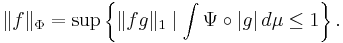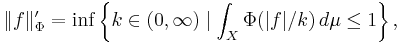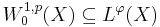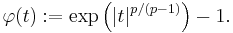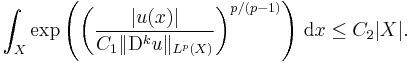Birnbaum–Orlicz space

In the mathematical analysis, and especially in real and harmonic analysis, a Birnbaum–Orlicz space is a type of function space which generalizes the L^p spaces. Like the L^p spaces, they are Banach spaces. The spaces are named for Władysław Orlicz and Zygmunt William Birnbaum, who first defined them in 1931.

Besides the L^p spaces, a variety of function spaces arising naturally in analysis are Birnbaum–Orlicz spaces. One such space L log⁺ L, which arises in the study of Hardy–Littlewood maximal functions, consists of measurable functions f such that the integral

$\int_{\mathbb{R}^n} |f(x)|\log^%2B |f(x)|\,dx < \infty.$

Here log⁺ is the positive part of the logarithm. Also included in the class of Birnbaum–Orlicz spaces are many of the most important Sobolev spaces.

1 Formal definition
2 Properties
3 Relations to Sobolev spaces
4 References

Formal definition

Suppose that μ is a σ-finite measure on a set X, and Φ : [0, ∞) → [0, ∞) is a convex function such that

$\frac{\Phi(x)}{x} \to \infty,\quad\mathrm{as\ \ }x\to \infty,$

$\frac{\Phi(x)}{x} \to 0,\quad\mathrm{as\ \ }x\to 0.$

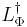Let $L^\dagger_\Phi$ be the space of measurable functions f : X → R such that the integral

$\int_X \Phi(|f|)\, d\mu$

is finite, where as usual functions that agree almost everywhere are identified.

This may not be a vector space (it may fail to be closed under scalar multiplication). The vector space of functions spanned by 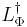$L^\dagger_\Phi$ is the Birnbaum–Orlicz space, denoted $L_\Phi$ .

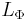To define a norm on 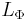$L_\Phi$ , let Ψ be the Young complement of Φ; that is,

$\Psi(x) = \int_0^x (\Phi')^{-1}(t)\, dt.$

Note that Young's inequality holds:

$ab\le \Phi(a) %2B \Psi(b).$

The norm is then given by

$\|f\|_\Phi = \sup\left\{\|fg\|_1\mid \int \Psi\circ |g|\, d\mu \le 1\right\}.$

Furthermore, the space 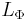$L_\Phi$ is precisely the space of measurable functions for which this norm is finite.

An equivalent norm (Rao & Ren 1991, §3.3) is defined on L_Φ by

$\|f\|'_\Phi = \inf\left\{k\in (0,\infty)\mid\int_X \Phi(|f|/k)\,d\mu\le 1\right\},$

and likewise L_Φ(μ) is the space of all measurable functions for which this norm is finite.

Properties

Orlicz spaces generalize L^p spaces in the sense that if 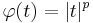$\varphi (t) = | t |^{p}$ , then 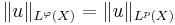$\| u \|_{L^{\varphi} (X)} = \| u \|_{L^{p} (X)}$ , so $L^{\varphi} (X) = L^{p} (X)$ .
The Orlicz space 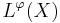$L^{\varphi} (X)$ is a Banach space — a complete normed vector space.

Relations to Sobolev spaces

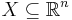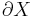Certain Sobolev spaces are embedded in Orlicz spaces: for $X \subseteq \mathbb{R}^{n}$ open and bounded with Lipschitz boundary $\partial X$ ,

$W_{0}^{1, p} (X) \subseteq L^{\varphi} (X)$

for

$\varphi (t)�:= \exp \left( | t |^{p / (p - 1)} \right) - 1.$

This is the analytical content of the Trudinger inequality: For 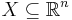$X \subseteq \mathbb{R}^{n}$ open and bounded with Lipschitz boundary 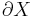$\partial X$ , consider the space 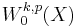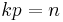$W_{0}^{k, p} (X)$ , $k p = n$ . There exist constants 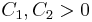$C_{1}, C_{2} > 0$ such that

$\int_{X} \exp \left( \left( \frac{| u(x) |}{C_{1} \| \mathrm{D}^{k} u \|_{L^{p} (X)}} \right)^{p / (p - 1)} \right) \, \mathrm{d} x \leq C_{2} | X |.$

References

Birnbaum, Z. W.; Orlicz, W. (1931), "Über die Verallgemeinerung des Begriffes der zueinander Konjugierten Potenzen", Studia Mathematica 3: 1–67 PDF.
Bund, Iracema (1975), "Birnbaum–Orlicz spaces of functions on groups", Pacific Mathematics Journal 58 (2): 351–359 .
Hewitt, Edwin; Stromberg, Karl, Real and abstract analysis, Springer-Verlag .
Krasnosel'skii, M.A.; Rutickii, Ya.B. (1961), Convex Functions and Orlicz Spaces, Groningen: P.Noordhoff Ltd
Rao, M.M.; Ren, Z.D. (1991), Theory of Orlicz Spaces, Pure and Applied Mathematics, Marcel Dekker, ISBN 0-8247-8478-2 .
Zygmund, Antoni, "Chapter IV: Classes of functions and Fourier series", Trigonometric series, Volume 1 (3rd ed.), Cambridge University Press .

Birnbaum–Orlicz space

Contents

Formal definition

Properties

Relations to Sobolev spaces

References